Bitwise Operators
Bitwise operators work on bits. They are divided into two categories – Bitwise Shift operators and Bitwise Logical Operators. First we will discuss shift operators.
Bitwise Shift Operators << and >>
The two shift operators are left shift and right shift. They are written as << and >>. The left shift operator moves (i.e. shifts) the bits of its operand to the left. The right shift operator moves the bits of its operand to the right. In left shift, the vacated bits on right are filled with zeros. In right shift, the vacated bits on left are filled with the sign bit.
Left Shift Operator
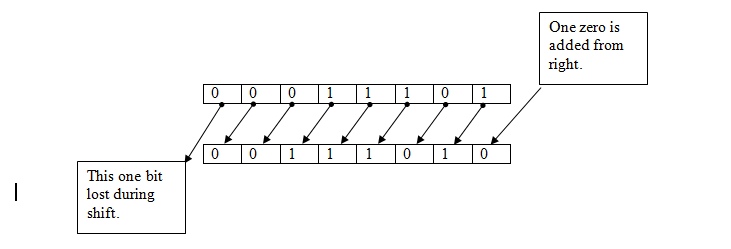
Consider a bit pattern 00011101, stored in a byte. When this pattern is shifted to left by one, using left shift operator <<, then each bit in pattern moves to left by one position. The leftmost one bit is lost and one zero added from right. This is shown here –
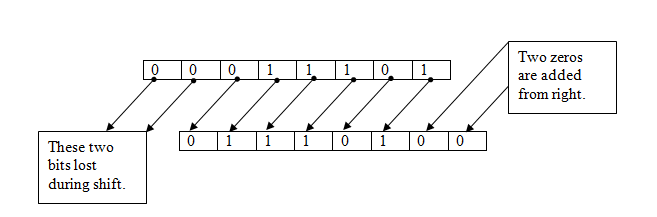
When the same bit pattern is shifted to left by two, each bit in pattern moves to left direction by two positions. And, two leftmost bits lost. Also, two zeros are added from right. This is shown here –
The binary equivalent of +1234 (or 1234) is 0000010011010010. Now understand how left shift operator works. On writing 1234 << 2, the left shift operator will shift all the bits of 1234 to left by 2 positions and the two vacated right bits are filled with zero. Mean to say, 1234 << 2 is actually 0000010011010010 << 2 which gives 0001001101001000 this is 4936. So, 1234 << 2 is equivalent to 1234 × 22 which gives 1234 × 4 = 4936.
The process is shown here with the help of diagram.
Similarly, 1234 << 3 shifts all the bits to left by 3 positions. The vacated 3 bits on right are filled with zeros as prescribed. Mean to say, 1234 << 3 is 0000010011010010 << 3 which gives 0010011010010000 i.e. 9872. So, 1234 << 3 is equivalent to 1234 × 23 which gives 1234 × 8 = 9872.
operand << position
Here, operand has a bit pattern and position is the position by which you want to shift each bit towards left.
Shifting the bits of an operand by N position is equivalent to multiply the operand by 2N. For example, 1234 << 3 gives 9872. Also 1234 × 23 = 9872. Thus, 1234 << 3 = 1234 × 23 which gives 1234 × 8 = 9872.
While using left shift operators, if the original value of the sign bit (which is the left most bit) changes, then the sign changes. In the above two examples 1234 << 2 and 1234 << 3 the value of sign bit remains 0 before and after the shift. So the results after the shift, 4936 and 9872, have the same sign as the operand 1234 i.e. positive. Consider one example more. 1234 << 5 will shift the bits by 5 positions. The left most five bits will lost and the left most sign bit will be 1. This will cause the result to be negative. 1234 << 5 is 0000010011010010 << 5 which gives 1001101001000000 this is -26048. In the result sign is negative, because, the value of the sign bit has been changed after the shift. By our formula 1234 << 5 is equal to 1234 × 25 = 1234 × 32 = 39488. Because 39488 exceed the range of integer, it is converted to fit into integer. For this, 65536 is subtracted from 39488 which gives -26048. This process is shown here –
If a negative number is operated with left shift operator and its sign bit, which is already 1, changes to zero, the result comes positive. For example, -1234 is 1000010011010010. Here sign bit is one. Now, 1234 << 1 shifts the bits in pattern to left by one position. The resulting pattern is 0000100110100100. Here sign bit is zero which denotes a positive number. The resulting bit pattern 0000100110100100 is actually 2468.
If a negative number is operated with left shift operator and its sign bit, which is already 1, changes to zero, the result comes positive. For example, -1234 is 1000010011010010. Here sign bit is one. Now, 1234 << 1 shifts the bits in pattern to left by one position. The resulting pattern is 0000100110100100. Here sign bit is zero which denotes a positive number. The resulting bit pattern 0000100110100100 is actually 2468.
Right Shift Operator
The right shift operator shift the bits of its operand to right by the position specified. The right most bits lost during shift. The main difference between left shift and right shift is that in left shift, vacated bits are filled with zeros only, but in right shift the vacated bits are filled with the value of sign bit i.e. in right shift the vacated bits are filled by either zeros or ones depending upon the value of sign bit. For example the bit patters for 1234 is 0000010011010010. Here sign bit is zero. If you write 1234 >> 3 then it will shift the bits to right by 3 positions and the three rightmost bits will lost. Further, the three vacated bits at left will be filled with zero because the sign bit is zero in original pattern. Therefore the result of 1234 >> 3 is 0000000010011010 which is 154. Now consider -1234. The bit pattern for -1234 is 1000010011010010. Here sign bit is one. So, if you write -1234 >> 3 then the three leftmost vacated bits will be filled with one because the sign bit in original pattern is 1. Therefore the result of -1234 >> 3 is 1111000010011010 which is –28826.These two examples are presented here.
B
Bitwise Logical Operators
The bitwise logical operators are bitwise AND, bitwise OR and bitwise XOR. These three are represented by &, | and ^ respectively. Each one is a binary operator. They work on the bit pattern of their operands. AND gives result 1 when both the bits are 1 otherwise it gives zero. OR gives 1, when at least one bit is 1. When both bits are zero it gives zero. XOR gives 1 when one bit is zero and other is one. If both are 1 or both are 0 it gives zero. (Just think 0 as false and 1 as true, you will understand easily.)
The following table shows the working of bitwise logical operators.
First bit
b1 |
Second bit
b2 |
AND
b1 & b2 |
OR
b1 | b2 |
XOR
b1 ^ b2 |
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
1
|
1
|
1
|
0
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
0
|
Now see, how bitwise logical operators works. Suppose x = 1234 and y = 5678. The binary equivalents of 1234 and 5678 are 0000010011010010 and 0001011000101110 respectively. Writing x & y will perform a bitwise AND operation between the bit patterns of 1234 and 5678. As shown here –
0000010011010010 0001011000101110 & operation on each pair of bits which are corresponding to each other
0000010000000010
The resulting bit pattern is 0000010000000010 which is 1026 in decimal. So result of x & y or 1234 & 5678 is 1026.
If we write x | y then it will perform an bitwise OR operation between the bit patterns of 1234 and 5678 as shown here –
0000010011010010 0001011000101110 | operation on each pair of bits which are corresponding to each other
0001011011111110 The resulting bit pattern is 0001011011111110 which is 5886 in decimal. So result of x | y or 1234 | 5678 is 5886.
Similarly, if we write x ^ y then it will perform an XOR operation between the bit patterns of 1234 and 5678. As shown here –
0000010011010010 0001011000101110 ^ operation on each pair of bits which are corresponding to each other
0001001011111100 The resulting bit pattern is 0001001011111100 which is 4860 in decimal.
So result of x ^ y or 1234 ^ 5678 is 4860.
Please note that bitwise logical operators don’t change their operands; they just use them and gives the result of the operation. Here is the program to show the working of bitwise logical operators.
/* Bitwise logical Operators */
#include<stdio.h>
#include<conio.h>
int main(void)
{
int x = 1234, y = 5678, z;
clrscr();
printf("x = %d y = %d\n",x,y);
z = x & y;
printf("x & y =%d\n",z);
z = x | y;
printf("x | y = %d\n",z);
z = x ^ y;
printf("x ^ y = %d\n",z); printf("x = %d y = %d\n",x,y);
getch();
return 0;
}
Output:
x = 1234 y = 5678
x & y = 1026
x | y = 5886
x ^ y = 4860
x = 1234 y = 5678
As you can see, no change has been made to x and y during bitwise logical operations. They are just used but not changed.
Bitwise Assignment Operators
The second subgroup of shorthand assignment operators is bitwise assignment operators. They are given here –
Operator
Name
<<=
Left shift assignment
>>=
Right assignment
&=
Bitwise AND assignment
|=
Bitwise OR assignment
^=
Bitwise XOR assignment
A Symbol can represent several operators
Depending upon the context, a symbol can represent different operators. For example, consider &. This symbol when attached to a variable denotes address of operator for example - &x and when used between two variables / values such as x & y denotes bitwise AND. When & is used in pair i.e. &&, it denotes logical AND as in x < y && x < z.




c प्रोग्राम कोडर्स के लिए भाषा के नमूने
ReplyDeleteफाइबोनैचि संख्या सी प्रोग्राम कोड